How To Find R In A Geometric Sequence

Geometric Sequences and Sums

Sequence

A Sequence is a fix of things (usually numbers) that are in order.

Geometric Sequences

In a Geometric Sequence each term is found by multiplying the previous term by a abiding.

Example:

i, 2, 4, 8, xvi, 32, 64, 128, 256 , ...

This sequence has a gene of 2 between each number.

Each term (except the offset term) is found by multiplying the previous term by 2.

In General we write a Geometric Sequence like this:

{a, ar, ar², ar³, ... }

where:

• a is the first term, and
• r is the factor between the terms (called the "common ratio")

Instance: {1,two,4,8,...}

The sequence starts at ane and doubles each time, and so

• a=i (the outset term)
• r=ii (the "mutual ratio" between terms is a doubling)

And we get:

{a, ar, arⁱⁱ, ar³, ... }

= {1, one×2, 1×2^two, one×twoⁱⁱⁱ, ... }

= {1, 2, iv, 8, ... }

But exist careful, r should not be 0:

• When r=0, we go the sequence {a,0,0,...} which is not geometric

The Rule

Nosotros can likewise calculate any term using the Rule:

10_n = ar^(n-1)

(We use "north-1" because ar⁰ is for the 1st term)

Example:

10, 30, 90, 270, 810, 2430, ...

This sequence has a factor of three betwixt each number.

The values of a and r are:

• a = 10 (the first term)
• r = 3 (the "common ratio")

The Dominion for whatever term is:

x_north = 10 × 3^(n-i)

So, the 4th term is:

x_iv = 10×iii^(4-i) = 10×three³ = x×27 = 270

And the 10th term is:

x₁₀ = 10×3^(10-ane) = 10×iii⁹ = 10×19683 = 196830

A Geometric Sequence can likewise have smaller and smaller values:

Example:

This sequence has a gene of 0.5 (a one-half) betwixt each number.

Its Dominion is 10_n = four × (0.5)^{due north-ane}

Why "Geometric" Sequence?

Because it is similar increasing the dimensions in geometry:

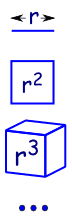	a line is i-dimensional and has a length of r
	in two dimensions a foursquare has an expanse of rii
	in 3 dimensions a cube has volume r3
	etc (yeah we tin can have 4 and more dimensions in mathematics).

Geometric Sequences are sometimes called Geometric Progressions (G.P.'s)

Summing a Geometric Series

To sum these:

a + ar + ar^two + ... + ar^{(due north-ane)}

(Each term is ar^k , where k starts at 0 and goes upwardly to due north-i)

We tin use this handy formula:

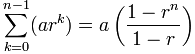
a is the first term
r is the "common ratio" betwixt terms
due north is the number of terms

What is that funny Σ symbol? It is chosen Sigma Notation

(called Sigma) ways "sum up"

And below and in a higher place it are shown the starting and ending values:

It says "Sum upward n where n goes from one to 4. Answer=10

The formula is easy to employ ... just "plug in" the values of a, r and northward

Example: Sum the outset iv terms of

ten, xxx, ninety, 270, 810, 2430, ...

This sequence has a gene of 3 betwixt each number.

The values of a, r and n are:

• a = 10 (the commencement term)
• r = 3 (the "mutual ratio")
• n = 4 (we want to sum the first 4 terms)

And then:

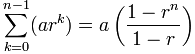
Becomes:

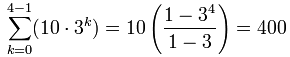
You tin can bank check it yourself:

x + 30 + 90 + 270 = 400

And, yes, it is easier to just add together them in this example, every bit in that location are but 4 terms. But imagine adding 50 terms ... then the formula is much easier.

Using the Formula

Let's see the formula in action:

Instance: Grains of Rice on a Chess Board

On the page Binary Digits we give an example of grains of rice on a chess lath. The question is asked:

When we place rice on a chess board:

• 1 grain on the showtime square,
• two grains on the second square,
• iv grains on the tertiary and and then on,
• ...

... doubling the grains of rice on each square ...

... how many grains of rice in full?

And then we accept:

• a = 1 (the starting time term)
• r = 2 (doubles each fourth dimension)
• n = 64 (64 squares on a chess board)

Then:

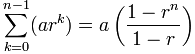
Becomes:

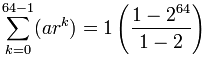
= 1−2⁶⁴ −ane = 2⁶⁴ − 1

= 18,446,744,073,709,551,615

Which was exactly the result we got on the Binary Digits page (give thanks goodness!)

And some other example, this time with r less than 1:

Example: Add upwards the commencement x terms of the Geometric Sequence that halves each time:

{ 1/ii, i/4, 1/8, i/16, ... }

The values of a, r and northward are:

• a = ½ (the first term)
• r = ½ (halves each time)
• n = 10 (10 terms to add)

And then:

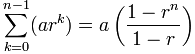
Becomes:

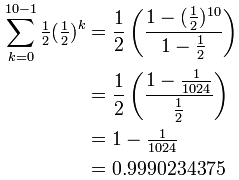
Very close to 1.

(Question: if we go along to increase n, what happens?)

Why Does the Formula Work?

Permit'due south meet why the formula works, considering we go to apply an interesting "trick" which is worth knowing.

Commencement, call the whole sum "S":   S = a + ar + arⁱⁱ + ... + ar^(north−2) + ar^(north−1)

Next, multiply S past r: South·r = ar + ar^two + ar³ + ... + ar⁽ⁿ⁻¹⁾ + arⁿ

Notice that S and S·r are similar?

At present decrease them!

Wow! All the terms in the middle neatly cancel out.
(Which is a not bad trick)

By subtracting S·r from Due south we get a simple consequence:

S − Due south·r = a − arⁿ

Allow'south rearrange it to find S:

Cistron out S and a: Due south(1−r) = a(1−rⁿ)

Dissever by (one−r): S = a(1−rⁿ) (1−r)

Which is our formula (ta-da!):

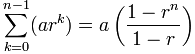
Space Geometric Serial

So what happens when northward goes to infinity?

We can use this formula:

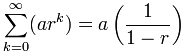
Simply be careful:

r must be between (only not including) −1 and 1

and r should not be 0 because the sequence {a,0,0,...} is non geometric

And then our infnite geometric series has a finite sum when the ratio is less than ane (and greater than −ane)

Let's bring dorsum our previous instance, and come across what happens:

Case: Add together upward ALL the terms of the Geometric Sequence that halves each time:

{ one 2 , i 4 , one 8 , 1 16 , ... }

We have:

• a = ½ (the first term)
• r = ½ (halves each fourth dimension)

And and then:

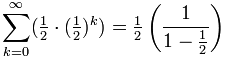
= ½×1 ½ = 1

Yes, adding ane 2 + 1 4 + 1 8 + ... etc equals exactly one.

Don't believe me? Only look at this foursquare: By adding up 1 2 + i four + 1 8 + ... we end upwardly with the whole thing!

Recurring Decimal

On another folio we asked "Does 0.999... equal 1?", well, let usa run into if we can summate it:

Example: Calculate 0.999...

We tin can write a recurring decimal as a sum like this:

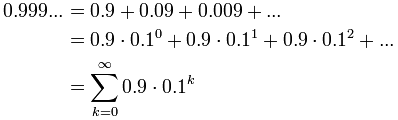
And now we can use the formula:

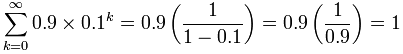
Yes! 0.999... does equal ane.

And so at that place nosotros have it ... Geometric Sequences (and their sums) can do all sorts of amazing and powerful things.

Source: https://www.mathsisfun.com/algebra/sequences-sums-geometric.html

Posted by: bukowskiolow1967.blogspot.com

Share this post