How To Use Tan To Find An Angle

This section looks at Sin, Cos and Tan inside the field of trigonometry.

A correct-angled triangle is a triangle in which 1 of the angles is a right-bending. The hypotenuse of a right angled triangle is the longest side, which is the one opposite the right bending. The adjacent side is the side which is betwixt the angle in question and the right angle. The reverse side is opposite the angle in question.

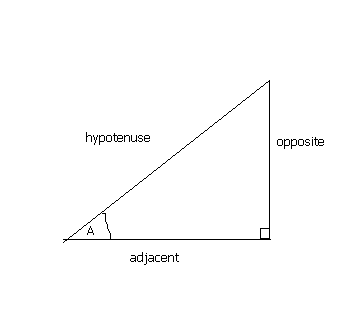
Sin Cos Tan

In any correct angled triangle, for whatsoever bending:

The sine of the angle = the length of the reverse side
the length of the hypotenuse

The cosine of the angle = the length of the side by side side
the length of the hypotenuse

The tangent of the angle = the length of the opposite side
the length of the adjacent side

And so in autograph annotation:
sin = o/h cos = a/h tan = o/a
Often remembered by: soh cah toa

Example

Find the length of side x in the diagram below:

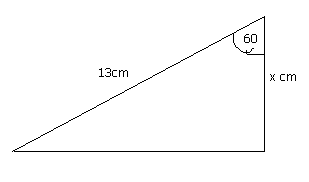
A right angled triangle

The angle is 60 degrees. We are given the hypotenuse and demand to notice the side by side side. This formula which connects these three is:
cos(angle) = adjacent / hypotenuse
therefore, cos60 = x / 13
therefore, ten = xiii × cos60 = vi.five
therefore the length of side x is 6.5cm.

This video will explain how the formulas work.

Trigonometry Video

The Graphs of Sin, Cos and Tan - (Higher TIER)

The following graphs show the value of sinø, cosø and tanø against ø (ø represents an angle). From the sin graph we can see that sinø = 0 when ø = 0 degrees, 180 degrees and 360 degrees.

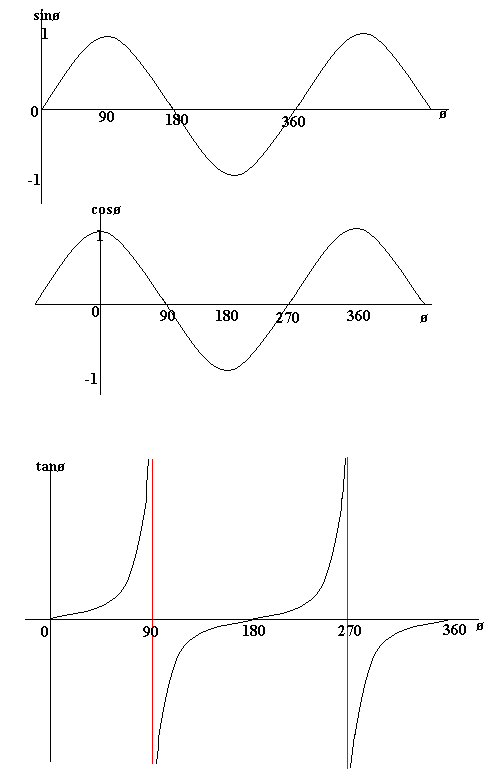
sin, cos and tan

Note that the graph of tan has asymptotes (lines which the graph gets close to, only never crosses). These are the red lines (they aren't actually function of the graph).

Also notice that the graphs of sin, cos and tan are periodic. This means that they repeat themselves. Therefore sin(ø) = sin(360 + ø), for example.

Observe also the symmetry of the graphs. For instance, cos is symmetrical in the y-centrality, which means that cosø = cos(-ø). And so, for example, cos(thirty) = cos(-30).
Also, sin ten = sin (180 - x) considering of the symmetry of sin in the line ø = 90.

For more information on trigonometry click here